Superefficiency

If you have $X_1,\dots ,X_n$ independent from an $N(\mu ,1)$ distribution you don’t have to think too hard to work out that ${\overline{X}}_n$, the sample mean, is the right estimator of $\mu$ (unless you have quite detailed prior knowledge). As people who have taken an advanced course in mathematical statistics will know, there is a famous estimator that appears to do better. 

Hodges’ estimator is given by $H_n={\overline{X}}_n$ if $|{\overline{X}}_n|>n^{-1/4}$, and $H_n=0$ if $|{\overline{X}}_n|\le n^{-1/4}$. If $\mu \ne 0$, $H_n={\overline{X}}_n$ for all large enough $n$, so $$\sqrt{n}(H_n-\mu )\stackrel{d}{\to }N(0,1)$$ just as for ${\overline{X}}_n$. On the other hand, if $\mu =0$, $$\sqrt{n}(H_n-\mu )\stackrel{p}{\to }0.$$ $H_n$ is asymptotically better than ${\overline{X}}_n$ for $\mu =0$ and asymptotically as good for any other value of $\mu$. Of course there’s something wrong with it: it sucks for $n^{-1/2}\ll \mu <n^{-1/4}$. Here’s its mean squared error:

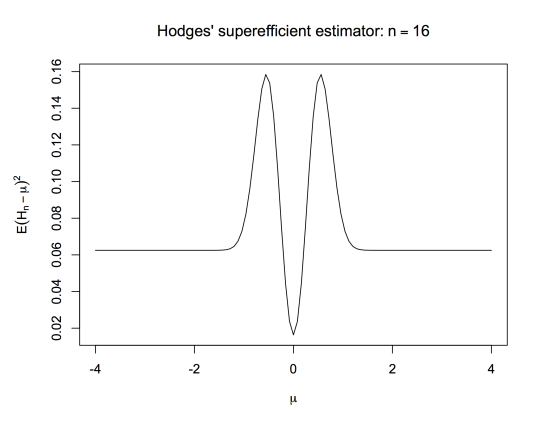
Even Wikipedia knows this much. What I recently got around to doing was extending this to an estimator that’s asymptotically superior to ${\overline{X}}_n$ on a dense set. This isn’t new – Le Cam did it in his PhD thesis. It may even be the same as Le Cam’s construction (which isn’t online, as far as I can tell). [Actually, Le Cam’s construction is a draft exercise in a draft chapter for David Pollard’s long-awaited ‘Asymptopia’. And it is basically my one, so it’s quite likely that as a Pollard fan I got at least the idea from there.]

First, instead of just setting the estimate to zero when it’s close enough to zero, we can set it to the nearest integer when it’s close enough to an integer.  Define ${\tilde{H}}_n=i$ if $|{\overline{X}}_n-i|<0.5n^{-1/4}$, with ${\tilde{H}}_n={\overline{X}}_n$ otherwise.

If $n$ is large enough, we can shrink to multiples of 1/2. For example, using the same threshold for closeness, if $n>16$ there is at most one multiple of 1/2 within $0.5n^{-1/4}$. If $n>256$ there is at most one multiple of 1/4 within that range.

Define $H_{n,k}=2^{-k}i$ if $|x-2^{-k}i|<0.5n^{-1/4}$ and $H_{n,k}={\overline{X}}_n$ otherwise. This is well-defined if $n>2^{4k}$. For any fixed $k$, ${\tilde{H}}_{n,k}$ satisfies $$\sqrt{n}(H_n-\mu )\stackrel{p}{\to }0$$ if $\mu$ is a multiple of $2^{-k}$ and $$\sqrt{n}(H_n-\mu )\stackrel{d}{\to }N(0,1)$$ otherwise.

The obvious thing to do now is to let $k$ increase slowly with $n$. This doesn’t work. Consider a value for $\mu$ whose binary expansion has infinitely many 1s, but with increasingly many zeroes between them. Whatever your rule for $k\left(n\right)$ there will be values of this type that are close enough to multiples of $2^{-k\left(n\right)}$ to get pulled to the wrong value infinitely often as $n$ increases. $H_{n,k\left(n\right)}$ will be asymptotically superior to ${\overline{X}}_n$ on a dense set, but it will be asymptotically inferior on another dense set, violating the rules of the game. 

What we can do is pick $k$ at random. The efficiency gain isn’t 100% as it was for fixed $k$, but it’s still there. 

Let $K$ be a random variable with probability mass function $p\left(k\right)$, independent of the $X$s.  The distribution of $H_{n,K}$ conditional on $K=k$ is the distribution of $H_{n,k}$. If $p\left(k\right)>0$ for all $k$, the probability  of seeing $K=k$ infinitely often is 1, so we can look the limiting distribution of $\sqrt{n}(H_{n,K}-\mu )$ along subsequences with $K=k$. This limiting distribution is a point mass at zero  if $2^k\mu$ is an integer, and $N(0,1)$ otherwise. So, $$\sqrt{n}(H_{n,K}-\mu )\stackrel{d}{\to }{q}_k{\delta }_0+(1-q_k)N(0,1)$$ where $$q_k=\sum _k{p}_{k}I\left(2^k\mu \text{is an integer}\right)$$

For a dense set of real numbers, and in particular for all numbers representable in binary floating point, $H_{n,K}$ has greater asymptotic efficiency than the efficient estimator ${\overline{X}}_n.$  The disadvantage of this randomised construction is that working out the finite-sample MSE is just horrible to think about.

The other interesting thing to think about is why the ‘overflow’ heuristic doesn’t work. Why doesn’t superefficiency for all fixed $k$ translate into superefficiency for sufficiently-slowly increasing $k\left(n\right)$? As a heuristic, this sort of thing has been around since the early days of analysis, but it’s more than that: the field of non-standard analysis is basically about making it rigorous. 

My guess is that $H_{n,k}$ for infinite $n$ is close to the superefficient distribution on the dense set only for ‘large enough’ infinite $k$, and close to $N(0,1)$ off the dense set only for ‘small enough’ infinite $k$. The failure of the heuristic is similar to the failure in Cauchy’s invalid proof that a convergent sequence of continuous functinons has a continuous limit, the proof into which later analysis retconned the concepts of ‘uniform convergence’ and ‘equicontinuity’.